Akasec CTF [HW] Alien Circuit

Description

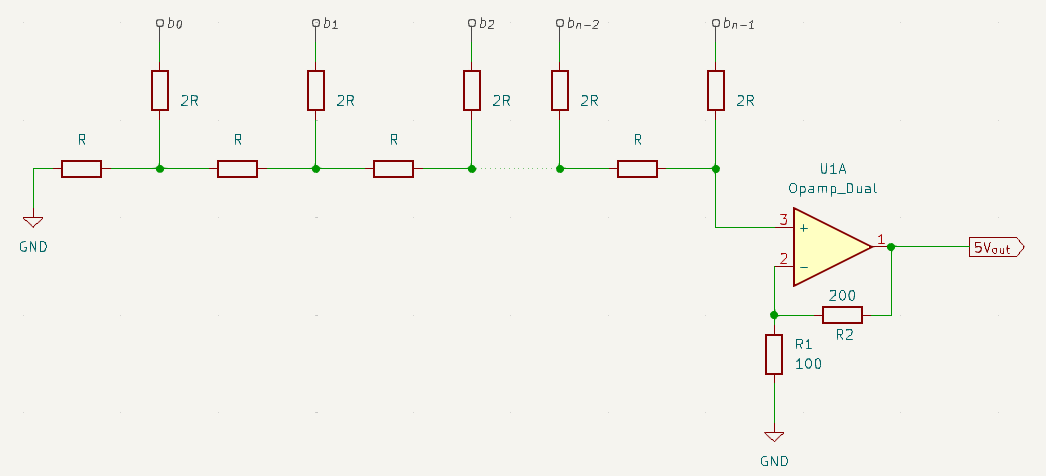
The following schematic was given with the challenge:

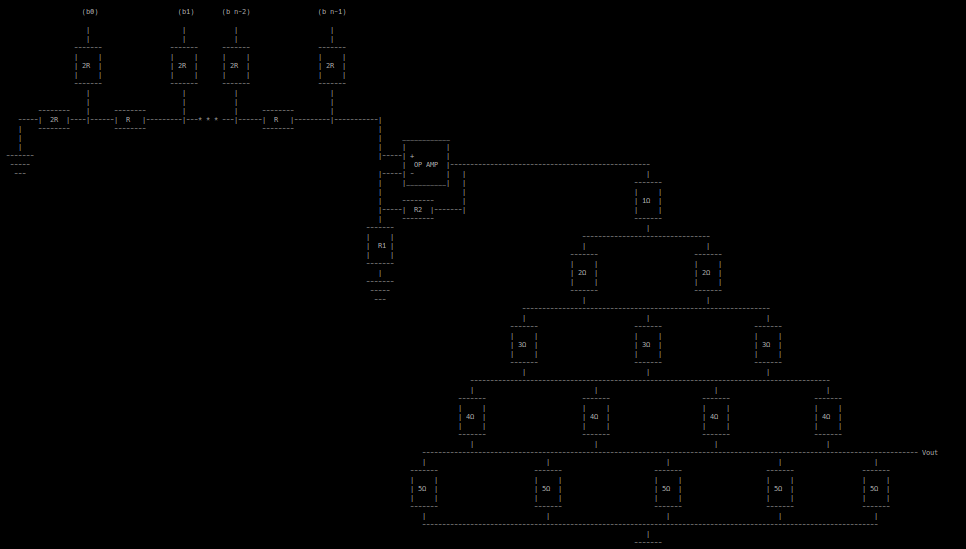
This information was included in the schematic:

Important Information:

bn (logic high = 3.3V)

R1 = 100Ω
R2 = 200Ω

Vout = 1.0100160293633633097836165218520645928533165673701591638847239768412297771673628701675769728865523783884907827854645836850813325581348710325049612453127737826117688733914936444315081605041365932902096V

Analysis

This challenge centers around a classic circuit: the R-2R ladder Digital-to-Analog Converter (DAC). If you’ve encountered these before, the path forward should be clear. If not, don’t fret! Plenty of online resources explain how R-2R ladders work.

To make things easier to grasp, I’ve reconstructed the provided circuit using KiCad.

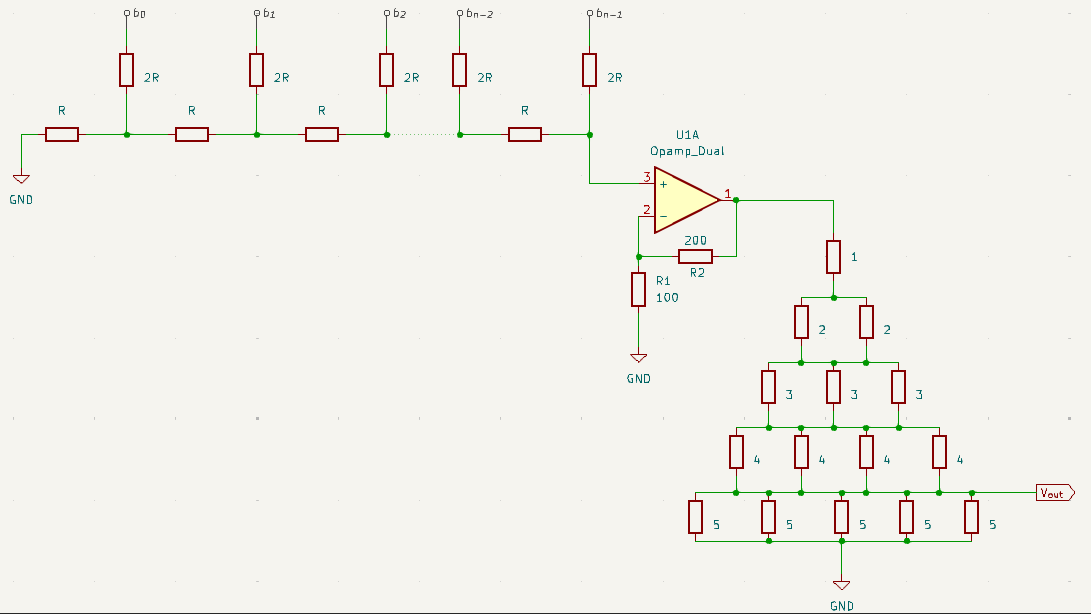
Our first step is to simplify this intimidating resistor network using basic series and parallel resistance calculations.

Now, let’s determine the voltage at the op-amp’s positive input (V+), which also happens to be the output voltage of the R-2R ladder ($V_{out0}$). Assuming an ideal op-amp, we know that:

$$V^{+}=V^{-}$$

and since the positive input is connected to the output:

$$V^{+}=V_{out0}$$

We can find $V_{out0}$ using Millman’s Theorem:

$$V_{out0}=\frac{\frac{5V_{out}}{R_2}}{\frac{1}{R_1}+\frac{1}{R_2}}=\frac{5V_{out}}{\frac{R_2}{R_1}+1}$$

Note that $5V_{out}$ represents the output voltage of the op-amp.

Finally, we arrive at the simplified expression for the R-2R ladder’s output:

$$V_{out0}=\frac{5V_{out}}{\frac{R_2}{R_1}+1}$$

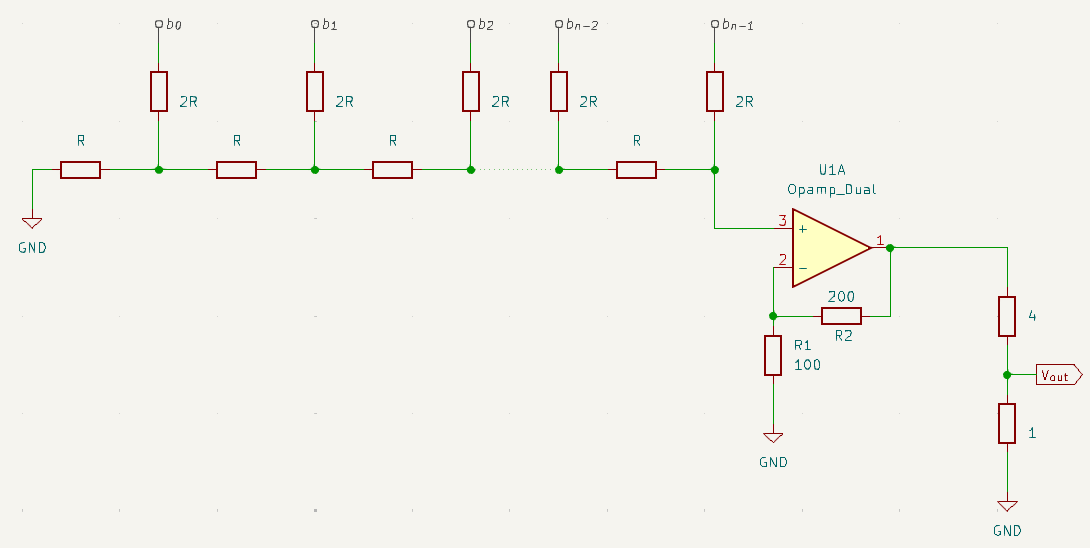
For further analysis, let’s isolate the R-2R ladder network, omitting the op-amp stage:

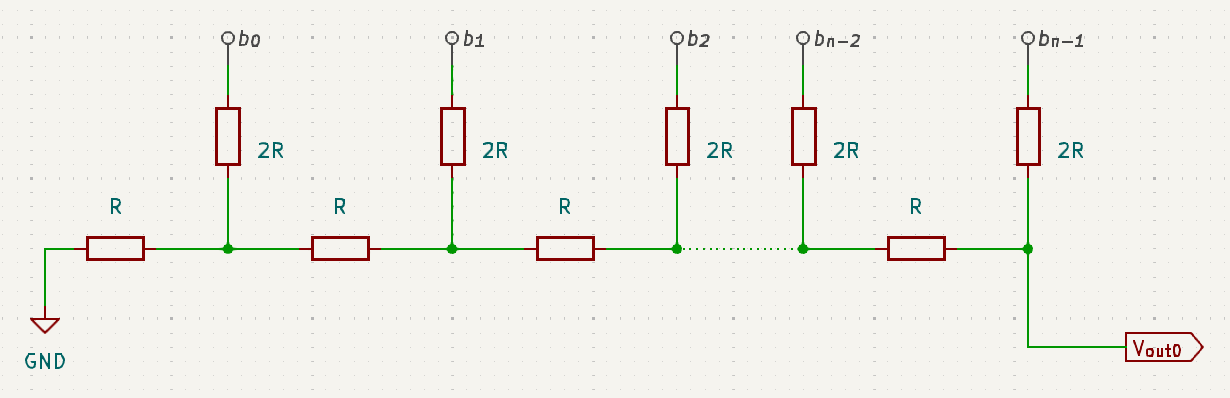
This simplified representation will be helpful as we try to recover the flag.

Solution

Understanding R-2R DAC Operation

Before passing to the solution first of all let’s understand how the R-2R DAC works. An R-2R DAC converts a digital input value into an analog voltage. The output voltage ($V_{out}$) is determined by the input voltages of each bit and follows this relationship:

$$V_{out}=\frac{V_0+2V_1+4V_2+...+2^n{V}_n}{2^n-1}$$

where:

• $V_i$ represents the input voltage for the corresponding bit i (0 or 1).
• $n$ is the number of bits.

In this scenario, the logic levels are defined by $V_{ref}=3.3V$. Therefore, $V_i$ will be either 3.3V (logic 1) or 0V (logic 0). We can simplify the equation to represent the digital input directly:

$$V_{out}=\frac{V_{ref}\times (b_0+2b_1+4b_2+8b_3+...+2^n{b}_n)}{2^n-1}$$

Here, $(b_0+2b_1+4b_2+8b_3+...+2^n{b}_n)$ represents the digital input value in binary. Rearranging the equation allows us to calculate this digital value based on the measured output voltage:

$$(b_0+2b_1+4b_2+8b_3+...+2^n{b}_n)=\frac{V_{out}}{V_{ref}}\times (2^n-1)$$

It’s important to note that $V_{out}$ in this context refers to the voltage at the output of the R-2R ladder network, not the final circuit output. We need to consider any additional circuitry, which in our case involves an inverting op-amp:

$$V_{out0}=\frac{5V_{out}}{\frac{R_2}{R_1}+1}$$

where:

• $V_{out0}$ is the the voltage at the output of the R-2R ladder network.
• $R_1$ and $R_2$ are the resistances in the inverting operational amplifier.

Python Implementation

To decode the flag, we’ll use Python. Due to the high precision required, we’ll use the decimal library:

from decimal import Decimal, getcontext
getcontext().prec = 300

Next, we define the known variables:

Vref = Decimal(3.3)
R1 = Decimal(100)
R2 = Decimal(200)
Vout = Decimal("1.0100160293633633097836165218520645928533165673701591638847239768412297771673628701675769728865523783884907827854645836850813325581348710325049612453127737826117688733914936444315081605041365932902096")

We calculate the voltage at the R-2R ladder output:

Vout0 = 5*Vout / Decimal((R2/R1) + 1)

Since the number of bits (n) is unknown, we define a function to test different values:

def a2d(V, n): # analog to digital
    max_digital_value = Decimal(2**n - 1)
    digital_value = (V / Vref) * max_digital_value
    return int(digital_value)

Finally, we iterate through a range of potential n values, converting the output voltage to a digital value and checking if it contains the flag:

for i in range(1024, 8, -1):
    h = hex(a2d(Vout0, i))[2:]
    res = bytes.fromhex(h)
    if b'akasec' in res.lower() and b'}' in res:
        print("Flag:", res[:res.index(b'}')+1].decode())
        break

This script will search for the flag within the decoded digital values and print it once found.

And here’s our flag:

Flag: AKASEC{r_2r_d4c_plu5_0p_4mp_plu5_r351570r_7r33_3qu4l5_fun}

And never forget Palestine will be free 🇵🇸.

Here’s the full script

from decimal import Decimal, getcontext
getcontext().prec = 300
 
Vref = Decimal(3.3)
R1 = Decimal(100)
R2 = Decimal(200)
Vout = Decimal("1.0100160293633633097836165218520645928533165673701591638847239768412297771673628701675769728865523783884907827854645836850813325581348710325049612453127737826117688733914936444315081605041365932902096")
 
Vout0 = 5*Vout / Decimal((R2/R1) + 1)
 
def a2d(V, n): # analog to digital
    max_digital_value = Decimal(2**n - 1)
    digital_value = (V / Vref) * max_digital_value
    return int(digital_value)
 
for i in range(1024, -1, -1):
    h = hex(a2d(Vout0, i))[2:]
    res = bytes.fromhex(h)
    if b'akasec' in res.lower() and b'}' in res:
        print("Flag:", res[:res.index(b'}')+1].decode())
        break